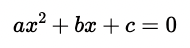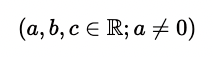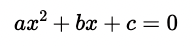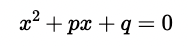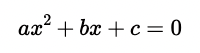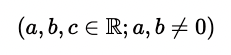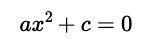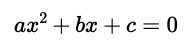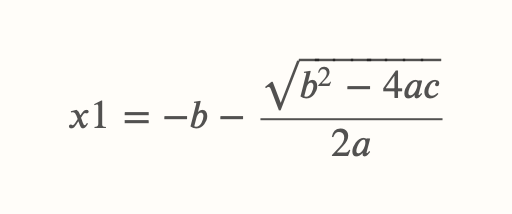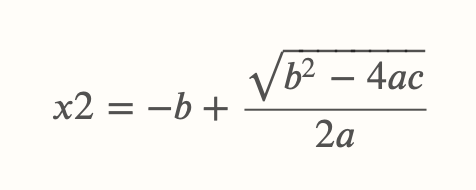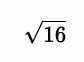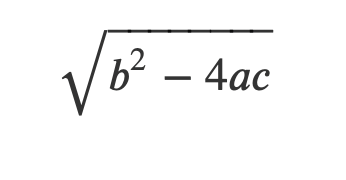Quadratische Gleichungen mit Python berechnen

Mathematische Grundlagen

Als quadratische Gleichungen werden Gleichungen bezeichnet, die folgende Form aufweisen:

Dabei gilt, dass a, b, c zur Menge der reellen Zahlen gehören und a ungleich Null ist:

Dabei wird zwischen zwei Arten der Darstellung unterschieden, je nach dem, ob der Koeffizient von $ x^2 $ gleich 1 ist.

Koeffizient ungleich 1:

Sofern der Koeffizient (Vorfaktor) von x² — also die Variable a — ungleich 1 ist, wird als Darstellungsform die allgemeine Form verwendet, mithin die bereits oben gezeigte Form:

Koeffizient gleich 1:

Sofern der Koeffizient gleich 1 ist, wird als Darstellungsform die Normalform verwendet:

Denn aufgrund des Umstands, dass 1 * x² = x² ist, kann der Koeffizient a weggelassen werden.

Eine quadratische Gleichung kann auf unterschiedliche Weise gelöst werden, je nachdem, ob eine allgemeine Form oder eine Normalform gegeben ist. Darüber hinaus, kommt es darauf an, ob das lineare Glied (bx bzw. px) vorhanden ist. Wenn es vorhanden ist, spricht man von einer gemischt-quadratischen Gleichung, also einer Gleichung der Form:

Dabei gilt:

Eine rein-quadratische Gleichung, also eine Gleichung ohne dem linearen Glied bx, würde hingegen wie folgt aussehen:

Lösung mit Python

Nach den mathematischen Grundlagen folgt jetzt die Lösung einer (gemischt-) quadratischen Gleichung

mithilfe von Python. Zur Lösung einer solchen Gleichung wird die abc-Formel (auch: Mitternachtsformel) verwendet. Sie ist die allgemeine Formel zur Lösung quadratischer Gleichungen, kann also auf alle Arten quadratischer Gleichungen angewendet werden. Für andere Arten als die der gemischt-quadratischen Gleichung gibt es darüber hinaus jedoch auch andere, einfachere Lösungswege, z.B. die pq-Formel als vereinfachte Variante für die Lösung quadratischer Gleichungen in Normalform.

Eine quadratische Gleichung kann keine, eine, oder zwei Lösungen haben. Hier die abc-Formel mit zwei Fallunterscheidungen:

und

Wenden wir uns damit dem Code zu. Es beginnt mit einer Import-Anweisung:

import math

Diese Bibliothek wird importiert, damit die zur Berechnung der Wurzel erforderliche Methode sqrt() verwendet werden kann.

Möchte man damit beispielsweise

berechnen, könnte das als Python-Code — in der IDLE — folgendermaßen aussehen:

>>> import math
>>> print(math.sqrt(16))
4.0

Der Ausdruck

ließe sich beispielsweise wie folgt berechnen:

result = math.sqrt(b**2 - 4 * a * c)

Definieren wir nun eine Funktion, die die abc-Formel abbildet:

def quadratic_formula(a, b, c):
    pass

Es erfolgt zunächst die Berechnung des Terms unter dem Wurzelzeichen:

disc = b**2 - 4 * a * c

Dieser Term wird als Diskriminante bezeichnet. Deshalb habe ich die Variable disc genannt.

Das Ergebnis dieser Berechnung wird nun verwendet, um die beiden Fallunterscheidungen zu berechnen:

x1 = (-b - math.sqrt(disc)) / (2 * a)
x2 = (-b + math.sqrt(disc)) / (2 * a)

Mit return werden die Ergebnisse zurückgegeben:

return(x1, x2)

Abschließend rufen wird die Funktion quadratic_formula() mit den zu übergebenden Argumenten auf und geben das Ergebnis aus:

result = quadratic_formula(2, -8, 6)
print(result)

Als Ergebnis erhält man für a = 2, b = -8 und c = 6 die Werte 1 und 3. Diese quadratische Gleichung hat also genau zwei Lösungen.

Anders sieht es bei folgenden Argumenten aus:

a = 2
b = -8
c = 8

Das zurückgegebene Tupel hat die Werte (2.0, 2.0). Dies bedeutet, dass es für diese quadratische Gleichung genau eine Lösung gibt.

Und schließlich führen die Werte

a = 2
b = -6
c = 11

zur Fehlermeldung ValueError: math domain error. In diesem Fall gibt es gar keine Lösung.

Hinsichtlich der Frage, ob keine, eine oder zwei Lösungen vorliegen, gilt übrigens folgendes:

Diskriminante < 0: keine Lösung
Diskriminante = 0: eine Lösung
Diskriminante > 0: keine Lösung

Hier der vollständige Code:

#!/usr/bin/env python3

import math

def quadratic_formula(a, b, c):

    disc = b**2 - 4 * a * c

    x1 = (-b - math.sqrt(disc)) / (2 * a)
    x2 = (-b + math.sqrt(disc)) / (2 * a)

    return(x1, x2)

result = quadratic_formula(2, -8, 6)
print(result)

Dieser Code ließe sich freilich noch verbessern. So wäre man deutlich flexibler, wenn man nach dem Start des Skripts nach den Werten für a, b und c gefragt werden würde. Sollte keine Lösung vorliegen, wäre darüber hinaus eine verständlichere Rückmeldung wünschenswert. Es sei Euch überlassen, die entsprechenden Anpassungen vorzunehmen.

Und es geht auch noch kürzer, wie folgender Code eines Lesers zeigt:

#!/usr/bin/env python3

import math


def quadratic_formula(a, b, c):

    x1 = (-b - math.sqrt(b * b - 4 * a * c)) / (2 * a)
    x2 = -b / a - x1

    return (x1, x2)


result = quadratic_formula(2, -8, 6)
print(result)

Grafische Darstellung

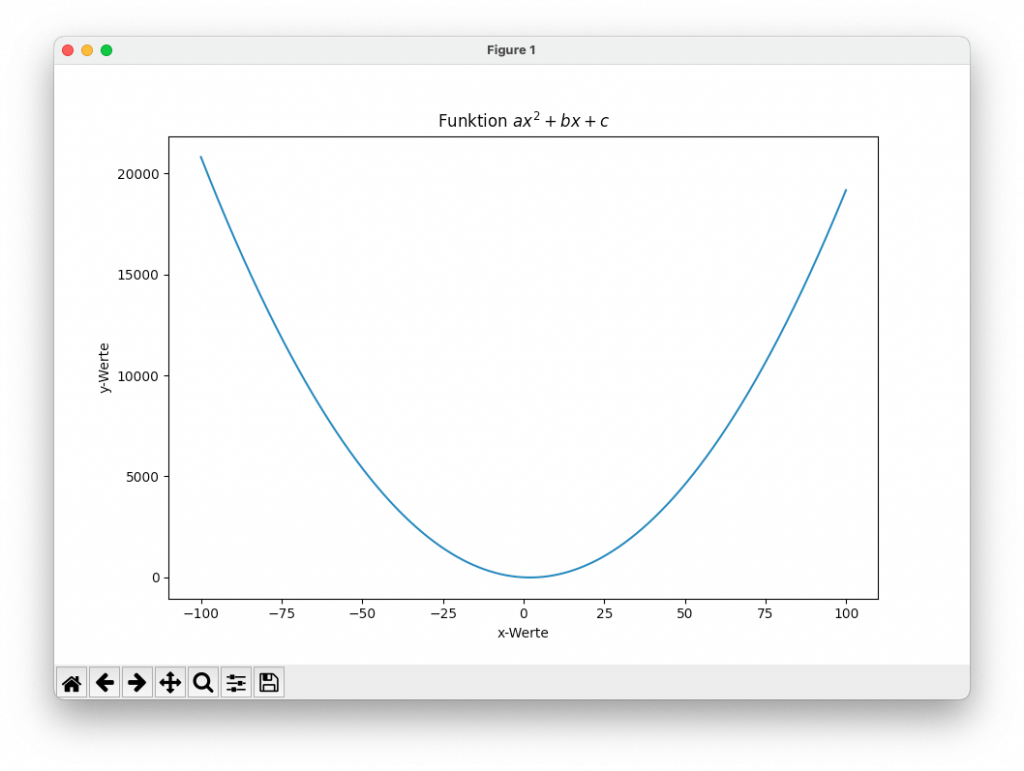
Mit Python und den Bibliotheken numpy und matplotlib kann zusätzlich eine grafische Darstellung erzeugt werden:

import numpy as np
import matplotlib.pyplot as plt

# Start: -100
# End: 100
# Steps: 0.1
x = np.arange(-100, 100, 0.1)
y = a * x**2 + b * x + c

plt.xlabel('x-Werte')
plt.ylabel('y-Werte')
plt.title('Funktion $ax^2 + bx + c$')

plt.plot(x, y)
plt.show()

Zuletzt aktualisiert am 24. November 2021