Eine baumartige Struktur trifft man in der Praxis vielerorts an. Man denke zum Beispiel an einen Familienstammbaum, an ein Organisationsdiagramm, an die Organisation eines Turniers oder an eine Mind Map.
Grundlagen
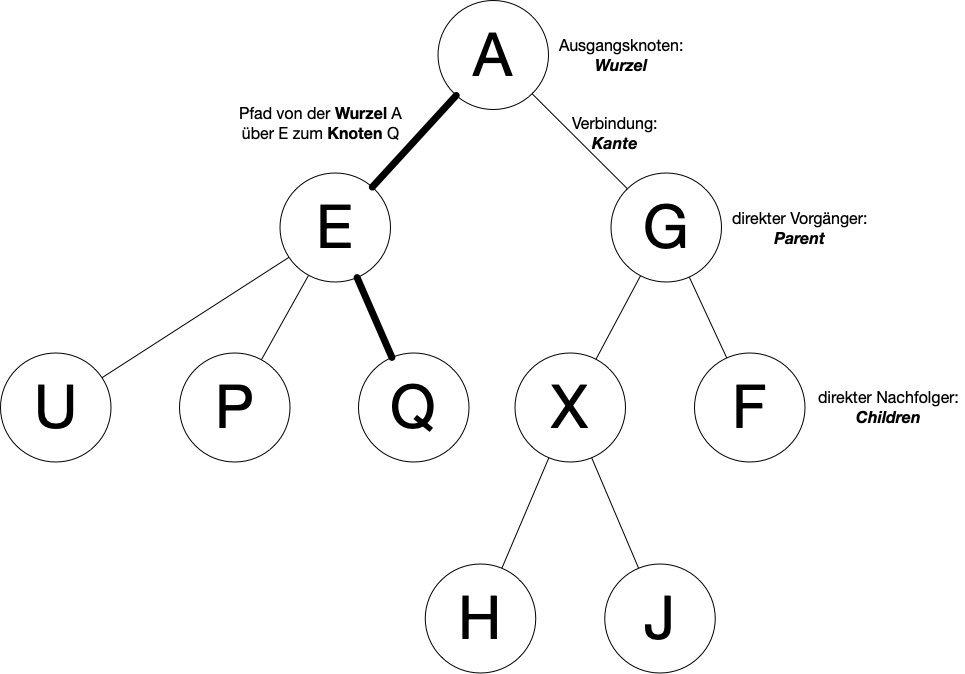
Auch in der Programmierung existiert eine Baum-Datenstruktur. Diese Datenstruktur ist einfach erklärt. Sie besteht aus Knoten (Nodes) und Kanten (Edges). Ein Knoten ist schlichtweg ein Objekt mit einer Bezeichnung (und evtl. weiteren mit ihm verknüpften Informationen). Knoten sind durch Kanten (Edges) miteinander verbunden. Ausgangspunkt der baumartigen Verzweigung ist dabei eine Wurzel (Root Node). Im Gegensatz zu einem Baum, wie man ihn aus der Natur kennt, ist die Wurzel der an oberster Stelle angeordnete Knoten. Nachfolgende Abbildung vermittelt die Struktur eines einfachen Baumes.
Bei der Verbindung von mehreren Knoten (hier: A über E zu Q) spricht man von einem Pfad. Des Weiteren wird ein Knoten, der der direkte Vorgänger eines anderen Knotens ist, als Parent (Parent Node) bezeichnet. Beim direkten Nachfolger handelt es sich dementsprechend um ein Children (Child Node).
Ein Knoten, der keine Child Nodes hat, wird als äußerer Knoten (Leaf Node) bezeichnet.
Binärer Baum
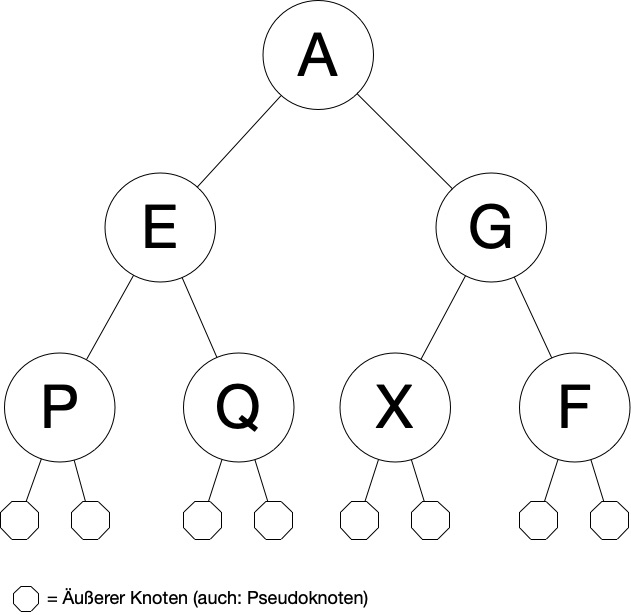
Die wohl einfachste Baumstruktur ist die eines binären Baums. Es handelt sich dabei um einen Baum, der aus äußeren Knoten ohne Nachfolger und aus inneren Knoten mit jeweils zwei Nachfolgern besteht. Binäre Baume sind in der Informatik von erheblicher Bedeutung.
Merke: Jeder binäre Baum ist ein Baum, aber nicht jeder Baum ist ein binärer Baum.
Von einem vollen binären Baum (Full Binary Tree) spricht man, wenn jede Ebene (mit Ausnahme der letzten Ebene) völlig mit inneren (also zwei) Knoten ausgefüllt ist oder keine Nachfolger hat. Bei dem Baum in der vorherstehenden Abbildung ist dies der Fall. In der Abbildung sind äußere Knoten (Leaf Nodes) besonders gekennzeichnet. Wie bereits erwähnt, haben sie keine Nachfolger (und hier auch keine Bezeichnung).
Algorithmen
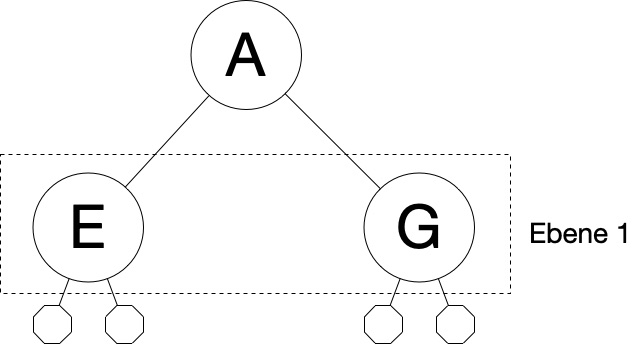
In der nachfolgenden Abbildung ist ein einfacher Baum dargestellt, der abgesehen von der Wurzel A aus einer Ebene 1 mit zwei inneren Knoten E und G besteht.
In der Programmiersprache Python läßt sich diese Baumstruktur als Code folgendermaßen darstellen, wobei hier davon ausgegangen wird, dass A = 72, E = 24 und G = 30 ist:
# A node class
class Node:
def __init__(self, data) -> None:
self.left = None
self.right = None
self.data = data
@property
def left(self):
return self.left
@left.setter
def left(self, left):
self.left = left
@property
def right(self):
return self.right
@right.setter
def right(self, right):
self.right = right
# Initialize a tree
root = Node(72)
# Add left and right node (E and G)
root.left = Node(24)
root.right = Node(30)Es sei angemerkt, dass in dieser Klasse explizit Getter und Setter bzw. die entsprechenden Decorators aufgeführt sind. Dies ist nicht zwangsläufig erforderlich, da Python hinsichtlich der Objektorientierten Programmierung keine strenge Datenkapselung fordert. Nichtsdestotrotz beschweren sich manche Editoren, wenn Getter und Setter nicht vorhanden sind, weswegen sie in diesem Beispiel hinzugefügt wurden.