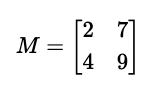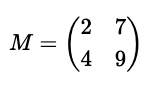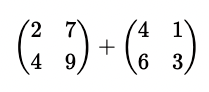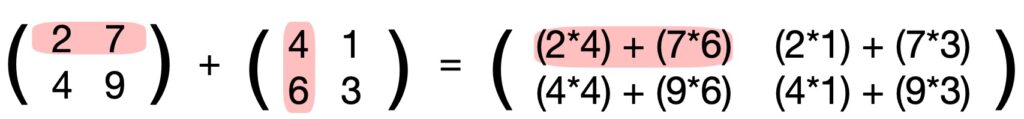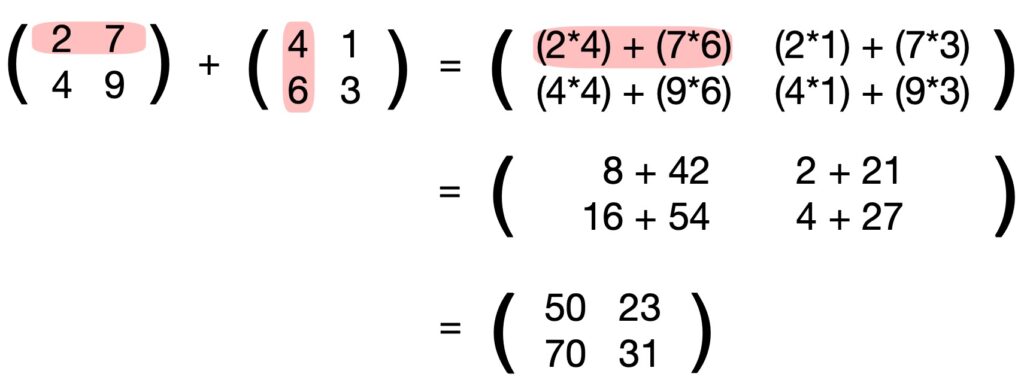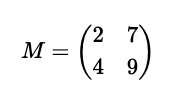Matrizenmultiplikation mit Python

Während mancher Mathestunde wird man sich gefragt haben, warum man sich mit Matrizenrechnung beschäftigen muss. Wenn man sich aber mit neuronalen Netzen (und Python) befasst, wird schnell klar, dass dieses Wissen von erheblicher praktischer Bedeutung ist. Grund genug, sich näher mit diesem Thema zu beschäftigen.

Was ist eine Matrix?

Darunter versteht man eine Anordnung von Zahlen in Zeilen und Spalten, mithin um eine Tabelle. Nachfolgend ein Beispiel für eine 2×2-Matrix mit ganzen Zahlen:

Da diese Matrix die gleiche Anzahl von Zeilen und Spalten enthält, wird sie als quadratische Matrix bezeichnet. Anstelle von eckigen Klammern, können auch runde Klammern verwendet werden:

Matrizen multiplizieren

Auf Matrizen lassen sich verschieden mathematische Operationen anwenden, zum Beispiel die Addition, die Subtraktion oder die Multiplikation, mit der wir uns hier beschäftigen wollen.

Damit sich zwei Matrizen multiplizieren lassen, muss die Anzahl der Spalten der ersten Matrix mit der Anzahl der Zeilen der zweiten Matrix übereinstimmen. Nachfolgend soll eine 2×2-Matrix mit einer 2×2-Matrix multipliziert werden, so dass diese Voraussetzung gegeben ist:

Die Multiplikation erfolgt nun dergestalt, dass die Zeilenelemente in der ersten Matrix mit den Spaltenelementen in der zweiten Matrix multipliziert werden. Für das obere linke Element in der Ergebnismatrix sieht dies wie folgt aus:

Die übrigen Elemente der Ergebnismatrix werden — wie dargestellt — ebenso berechnet, so dass dies zu folgendem Ergebnis führt:

Multiplikation mit Python und NumPy

Nachdem nun der Grundstein gelegt ist, kommen wir zu der Frage, wie dies mit Python gelöst werden kann. Es bietet sich an, hierfür auf das Paket NumPy zurückzugreifen.

Wenn wir von einer Matrix sprechen, dann haben wir es mit mehrdimensionalen Arrays zu tun. Betrachten wir nochmals die Ausgangsmatrix:

Hierbei handelt es sich um zwei Listen

a = [2, 7]
b = [4, 9]

die zu einer Matrix „verschmelzen“:

matrix1 = np.array([a, b])

Ebenso verhält es sich mit der zweiten Matrix:

c = [4, 1]
d = [6, 3]
matrix2 = np.array[c, d]

Die separate Erzeugung der Listen könnte man sich übrigens auch sparen:

matrix1 = np.array([[2, 7], [4, 9]])
matrix2 = np.array([[4, 1], [6, 3]])

Hinsichtlich der beiden Matrizen wird die Datenstruktur np.array aus dem Paket NumPy verwendet. Dies ermöglicht es uns, die Methode np.dot() anzuwenden, mit der eine Matrix-Multiplikation durchgeführt werden kann:

result = np.dot(matrix1, matrix2)

Der vollständige Code könnte wie folgt aussehen:

matrix1 = np.array([[2, 7], [4, 9]])
matrix2 = np.array([[4, 1], [6, 3]])
print(np.dot(matrix1, matrix2))

Als Ergebnis erhalten wir dann:

[[50 23]
 [70 31]]