Unabhängig davon, ob man sich das Programmieren im Selbststudium beibringt oder ob man im Informatikstudium damit konfrontiert wird, irgendwann trifft man auf die Big-O-Notation.
Was ist die Big-O-Notation?
Aber was versteht man unter der Big-O-Notation? Bei der Entwicklung bzw. der Auswahl eines Algorithmus kommt es auf die Frage an, wie schnell dieser ist. Hinsichtlich der Geschwindigkeit, wie auch der Größe des verwendeten Speichers, wird als Indikator die Big-O-Notation verwendet.
Dies ermöglicht eine Aussage darüber,
- wie performant ein Algorithmus ist, wenn sich die Zahl der durchzuführenden Aufgaben erhöht und
- wie der Algorithmus hinsichtlich der Geschwindigkeit und der Speichernutzung im Vergleich zu anderen Algorithmen abschneidet.
Nachfolgende Tabelle gibt eine Auskunft über die verwendeten Big-O-Werte:
| Big-O-Notation | Bezeichnung | Beschreibung |
|---|---|---|
| O(1) | konstant | Dies ist der best mögliche Wert. Es bedeutet, dass der Algorithmus stets die gleiche Zeit benötigt, unabhängig davon, wie viele Daten verarbeitet werden müssen. |
| O(log n) | logarithmisch | Dies ist ein ziemlich guter Wert. Diese Art von Algorithmen halbieren die vorhanden Daten bei jedem Durchlauf (Beispiel: Binär-Suche). Selbst bei einer großen Datenmenge ist ein solcher Algorithmus sehr schnell. |
| O(n) | linear | Auch dieser Algorithmus hat eine gute Performance. Eine Verdopplung der vorhanden Daten führt zu eine Verdoppelung der benötigten Zeit (Beispiel: Sequentielle Suche) |
| O(n log n) | loglinear | Dies ist ein noch annehmbarer Wert, wenn auch nicht so gut wie bei der linearen Big-O-Notation. |
| O(n2) | quadratisch | Von nun an geht es “den Bach runter”. Dieser Algorithmus ist langsam. Eine Verdoppelung der vorhandenen Daten führt zu einer Vervierfachung der aufzuwendenden Zeit. (Beispiel: Algorithmen, die verschachtelte Schleifen verwenden.) |
| O(n3) | kubisch | Dies ist eine schlechte Performance. Eine Verdoppelung der Daten führt zu einer Verachtfachung der Zeit. |
| O(2n) | exponentiell | Und es wird nicht besser. Diese Algorithmen sollte man eher vermeiden. Nur das Hinzufügen eines Bits verdoppelt die aufzuwendende Zeit. |
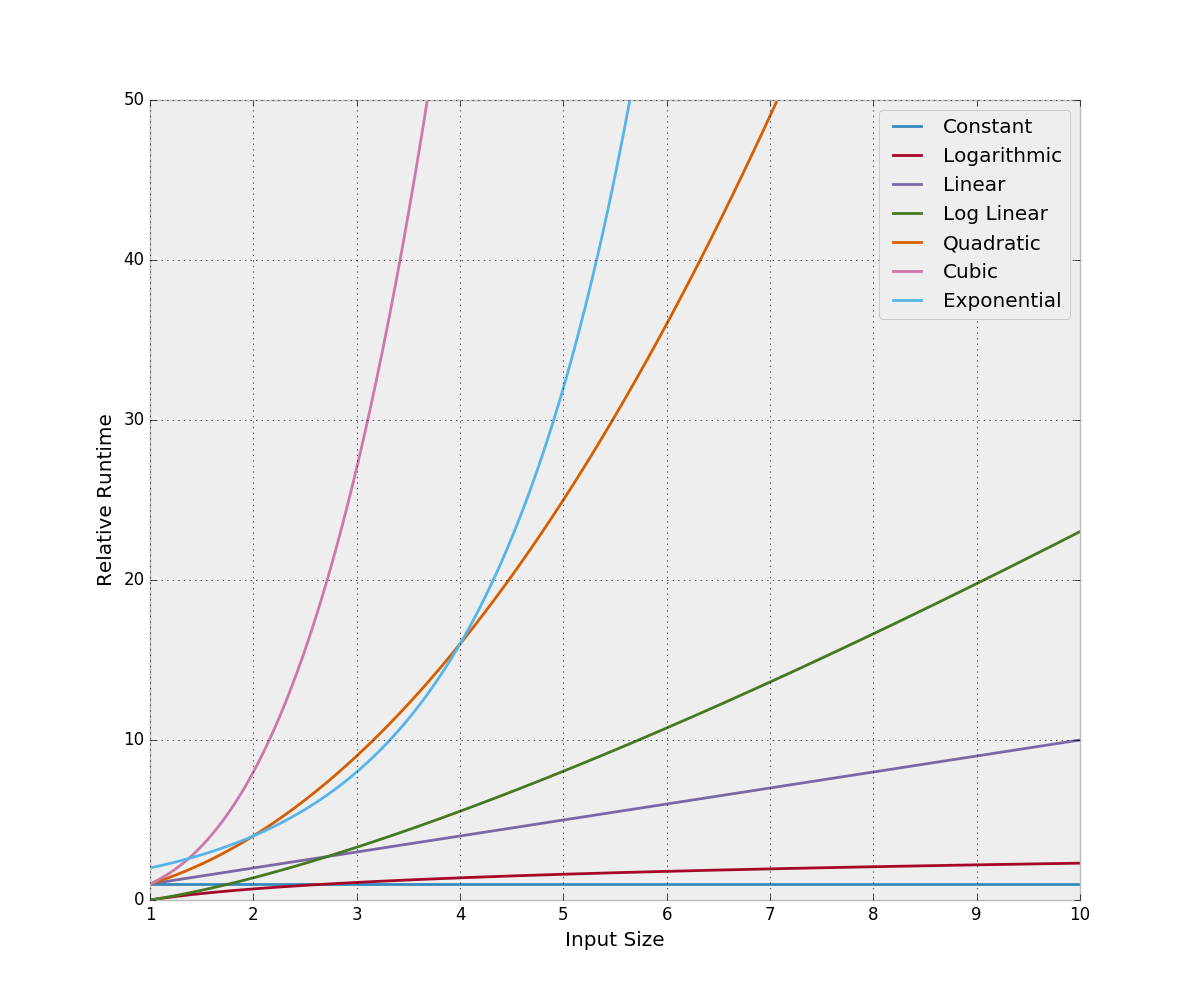
Nachfolgende Abbildung verdeutlicht die Big-O-Werte grafisch.
Als Faustformel für die Praxis kann man sich merken, dass ein Algorithmus, der über alle n-Elemente einer Eingabe in einer Schleife iteriert, den Wert O(n) hat. Bei zwei verschachtelten Schleifen ist man beim Wert O(n2), bei drei verschachtelten Schleifen bei O(n3), usw.
Man sollte aber bedenken, dass die Orientierung anhand der Big-O-Notation nur bei einer sehr hohen Anzahl von n-Elementen aussagekräftig ist.
Anmerkung: Die Grafik wurde übrigens mit Python und matplotlib erstellt. Den Code dafür könnt Ihr Euch bei Github ansehen.
Zuletzt aktualisiert am 11. Juli 2020